Decodificadores con entrada de habilitación

Supongamos que diseñamos  un decodificador de 2 entradas B, A y con 4 salidas Y0,Y1,Y2,Y3, el cual dispone además de una entrada de habilitación (Enable): G. Veamos cual es la función de esa entrada de habilitación.


En la hoja de datos ( data sheet)  del chip se tendría una tabla de funcionamiento, con niveles lógicos altos y
bajos, (HIGH y LOW), como se muestra a continuación:

 INPUTS        OUTPUTS

G   B   A      Y0   Y1   Y2   Y3
L    L    L       L     H    H     H
L    L    H      H     L     H     H
L    H    L      H     H     L     H
L    H    H      H     H     H     L
H    X   X       H     H     H    H


La Tabla de verdad en Lógica Positiva (H=1, L=0)  es la siguiente:


 Entradas            Salidas
G   B   A      Y0   Y1   Y2   Y3
0    0    0       0      1     1      1
0    0    1       1      0     1      1
0    1    0       1      1     0      1
0    1    1       1      1     1      0
1    X   X       1      1     1      1

Interpretando la tabla de verdad deducimos que para que el decodificador trabaje generando un CERO en la respectiva salida, la entrada de habilitación debe estar también a tierra ( G = 0). Si G = 1, todas las 4 salidas Y0,Y1,Y2,Y3 quedan en nivel alto,o UNOS, indicando  que el decodificador está deshabilitado.

Las ecuaciones Booleanas serán:     Y0' =G' B' A'  de donde Y0 = G + B + A (Aplicando teorema de De Morgan).

Así mismo:  Y1' =G' B' A   de donde Y1 = G + B +  A'
                   Y2' =G' B A'   de donde Y2 = G + B' + A
                   Y3' =G' B  A   de donde Y3 = G + B' + A'

La siguiente gráfica muestra un decodificador de 2 entradas/4 salidas con Enable, donde el Enable ahora se denomina E, las entradas A1 y A0, y las salidas ahora se llaman 0o,01,02,03.

Para implementar el circuito  lógico requerimos de 4 compuertas NAND de 3 entradas cada una, tal como se muestra, teniendo en cuenta que en una compuerta NAND sólamente cuando todas sus entradas están en nivel alto su salida es de nivel bajo.
Con  dos  decodificadores de 2 entradas /  4 salidas como el diseñado podemos implementar un decodificador de 3 entradas/ 8 salidas,  utilizando la entrada de habilitación o  Enable como el bit mas significativo. Podemos hacer  G = C.

Veamos la nueva tabla:

C  B  A     Y0   Y1  Y2   Y3   Y4   Y5   Y6   Y7
0   0   0      0      1     1      1     1       1     1      1  
0   0   1      1      0     1      1     1       1     1      1  
0   1   0      1      1     0      1     1       1     1      1  
0   1   1      1      1     1      0     1       1     1      1  
1   0   0      1      1     1      1     0       1     1      1  
1   0   1      1      1     1      1     1       0     1      1  
1   1   0      1      1     1      1     1       1     0      1  
1   1   1      1      1     1      1     1       1     1      0  

Observe que  si  puenteamos  B y  A en los decodificadores,  y  utilizamos un inversor conectado al Enable del segundo decodificador ( salidasY4,Y5,Y6,Y7), estando  C  directamente a la entrada G del primer decodificador que maneje las salidas Y0,Y1,Y2,Y3,logramos implementar  el decodificador de 3entradas/ 8 salidas, que nos permite encender de uno a la vez, 8 LEDS en configuración Anodo Común, tal como se muestra en la siguiente figura:
Este decodificador de 3 entradas/8 salidas trabaja en forma similar a como lo hace el 74138:

Verificamos que se cumple la tabla de Verdad :

                      ENTRADAS                                              SALIDAS      

                        C    B    A                      Y0     Y1     Y2     Y3     Y4       Y5     Y6     Y7
                         0    0     0                      0       1       1        1       1        1        1       1   
                         0    0     1                      1       0       1        1       1        1        1       1
                         0    1     0                      1       1       0        1       1        1        1       1   
                         0    1     1                      1       1       1        0       1        1        1       1
                         1    0     0                      1       1       1        1       0        1        1       1
                         1    0     1                      1       1       1        1       1        0        1       1
                         1    1     0                      1       1       1        1       1        1        0       1
                         1    1     1                      1       1       1        1       1        1        1       0        
  

Una  conclusión muy importante  que obtenemos es que: La entrada de habilitación es la que nos permite efectuar  la expansión.   

EJERCICIO:
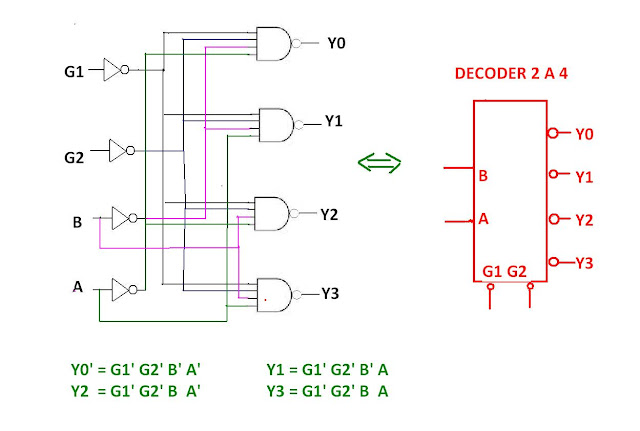
Diseñe un decodificador con 2 entradas de habilitación , 2 entradas / 4 salidas, de tal manera que con 4  de estos decodificadores  se puede implementar uno mas grande de 4 entradas / 16 salidas.

(a) Elabore su tabla de verdad, teniendo en cuenta que sus dos entradas de habilitación G1 y G2 son activas en nivel bajo  y sus cuatro salidas Y0,Y1,Y2,Y3 también son activas en nivel bajo.

(b) Escriba las 4 ecuaciones en Suma de Productos.

(c) Utilizando 4 compuertas NAND de 4 entradas y 4 inversores dibuje el circuito lógico. 

(d) Si se requiere implementar un decodificador de 4 entradas D,C,B,A   y  16 salidas activas en nivel  Bajo Y0,Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8,Y9,Y10,Y11,Y12,Y13,Y14,Y15 , indique gráficamente como se implementa el decodificador 4/16 usando cuatro decodificadores de 2/4 por Usted diseñados y  2  inversores adicionales.

Solución:

(a) Tabla de verdad:

 Entradas            Salidas
G1  G2    B   A      Y0   Y1   Y2   Y3
0     0       0    0       0      1     1      1
0     0       0    1       1      0     1      1
0     0       1    0       1      1     0      1
0     0       1    1       1      1     1      0
0     1      X   X       1      1     1      1
1     0      X   X       1      1     1      1
1     1      X   X       1      1     1      1

(b) Las ecuaciones Booleanas las obtenemos a partir del CERO lógico así:

Y0' = (G1' G2' B' A' ), de donde Y0 = G1 + G2 + B + A ( Aplicando Teorema de De Morgan)
Y1' = (G1' G2' B' A ), de donde Y1 = G1 + G2 + B + A'
Y2' = (G1' G2' B A' ), de donde Y2 = G1 + G2 + B' + A
Y3' = (G1' G2' B A ), de donde  Y3= G1 + G2 + B' + A'  

( c ) Circuito lógico:

( d ) Decoder 4 a 16  implementado con 4 decoder de 2 a 4:

El lector puede apreciar la importancia de las entradas de habilitación. Entre más "ENABLE" posea el decodificador mayor posibilidad de expansión se puede lograr.